Loop Subdivision

• 03 February 2022
• computer graphics

For the undergraduate computer graphics course (CMSC427) last semester, we were given an optional bonus assignment. We were required to implement some additional functionality in a 3D rendering engine, and I chose Loop subdivision.

Subdivision Surfaces #

Loop subdivision (not to be confused with the Loop Subdivide tool in Blender) is a subdivision scheme for triangle meshes. Subdivision surface algorithms are used to take a coarse mesh and generate a much smoother one. This is extremely useful for 3D modeling and for creating a high poly mesh for sculpting. The disadvantage is that each level of subdivision increases the triangle count by some multiplicative factor (4, in the case of Loop subdivision). This typically makes subdivision unsuitable for animating models, since you usually want around 30k polygons or less (unless you apply "hacks" like shadow baking to make your model look good).

Note that in Blender, since 3D artists typically prefer quads over tris in manual modeling, the Catmull-Clark algorithm is used instead. Quad meshes are better because it allows you to do loop cuts cleanly.

Winged Edge Data Structure #

Specialized data structures are needed for these subdivision surface algorithms, in this case the winged edge data structure. This data structure stores a list of vertices, edges, and faces, but in some sense the edges are most important. Each edge stores a reference to its four incident vertices and two faces (in some specified order). Each vertex only needs to store one incident edge (along with its coordinate position, of course). Each face only needs to store one incident edge.

One way to create this winged edge data structure is to loop through all the faces, but then looping through all edges is required to make sure edges are not duplicated. It might be possible to avoid this by first adding all vertices and edges, making sure not to duplicate edges by using a hashmap. Then, you can fill out the incident faces and edges for each edge. However, as a disclaimer, I did not thoroughly test this alternate implementation.

Loop Subdivision #

The Loop subdivision surface scheme basically takes each vertex in the original mesh and replaces it with a new vertex that is some convex combination of adjacent vertices. If $n$ is the degree of the vertex to be replaced, the weight $\beta$ for each of the adjacent vertices is $$\beta=\begin{cases} \frac{3}{8n}, \qquad n>3, \newline \frac{3}{16}, \qquad n=3. \end{cases}$$

An additional vertex is also added for each edge in the original mesh. If the edge has two incident faces, the new vertex is a convex combination of the four vertices comprising those two faces. The weights for the two "close" vertices on the edge are each $3/8$, while the weights for the two "far" vertices are each $1/8$.

If the edge only has a single incident face, then the new vertex is simply placed at the midpoint of the vertices making up that edge.

Finally, the only thing left to do is to fill in the faces.

This algorithm is actually quite simple and the more challenging part, surprisingly, is implementing the winged edge data structure.

Below are 5 levels of Loop subdivision applied onto a tetrahedron and an icosahedron.

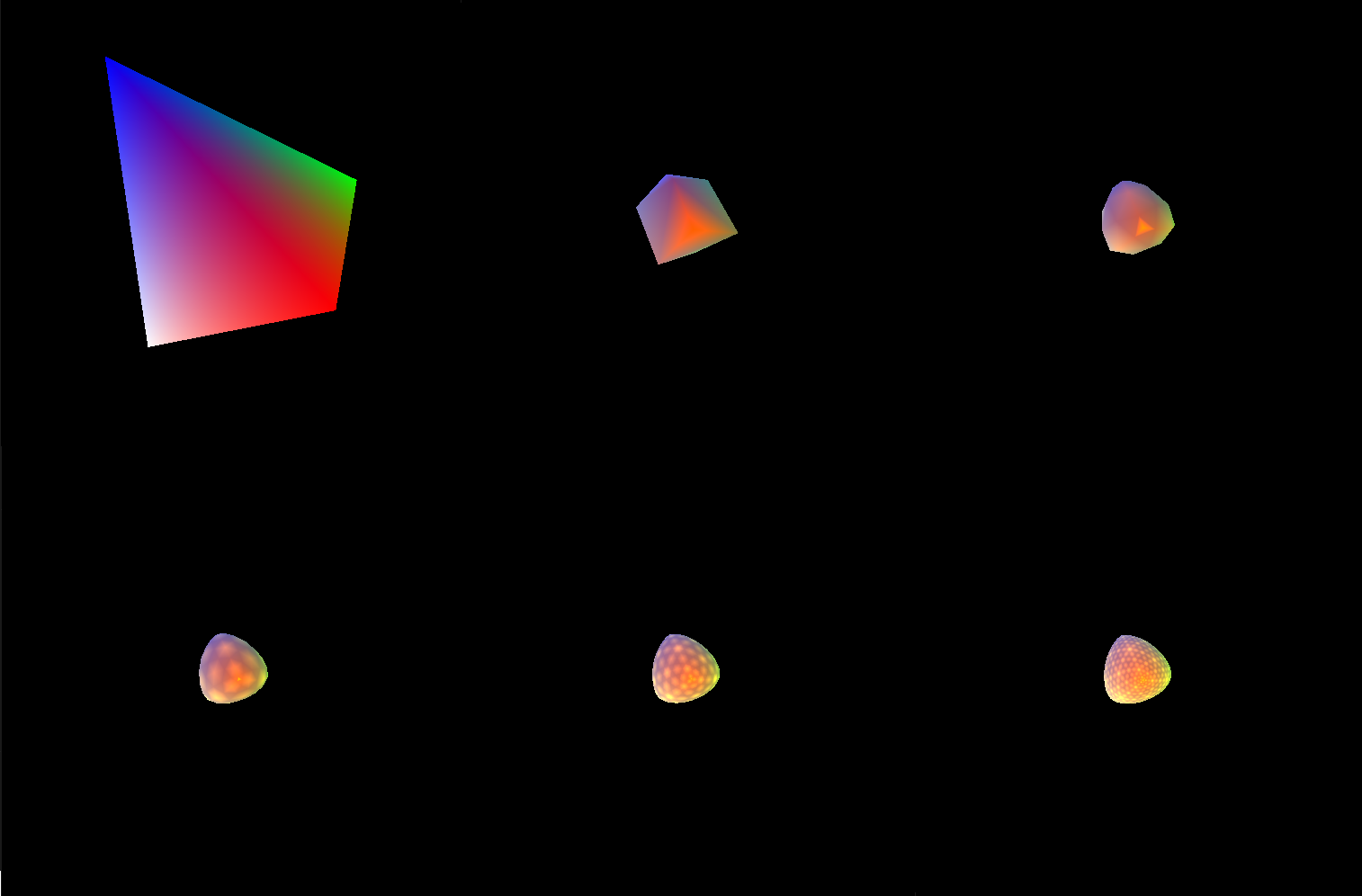
• Previous: Weak Duality for QP